The Monty Hall Problem
The Monty Hall problem is a statistical brainteaser and is based on a challenge from an old game show called “let’s make a deal” and named after it’s host, Monty Hall.
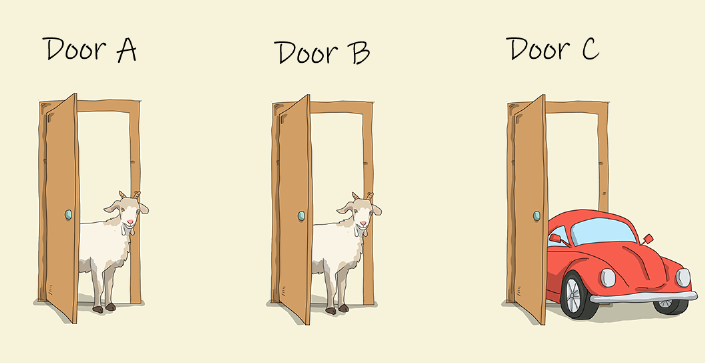
The Monty Hall problem is a statistical brainteaser and is based on a challenge from an old game show called “let’s make a deal” and named after it’s host, Monty Hall.
In the game show, the contestant is given three doors to choose from. Behind one door is a car, and behind the other two are goats. The host knows in advance what is behind each door. Once the contestant has chosen a door, the host will open one of the remaining doors that has a goat, then ask the contestant if he/she wants to switch to the remaining door.
Is it better for the contestant to switch or stay with their original choice?
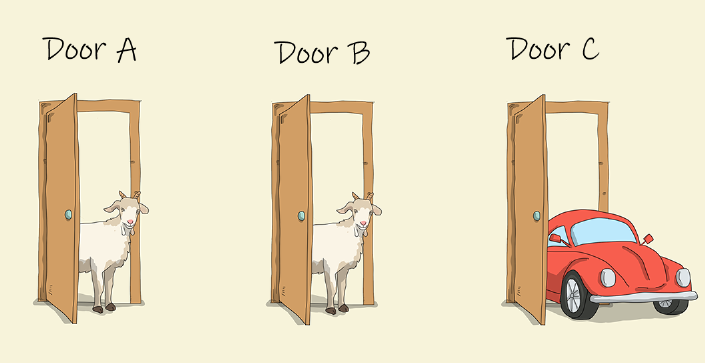
At first glance, it might seem that there is no advantage to switching, as showing the door with a goat will leave only two doors left unopened. Since you know one is a goat and the other the car, the odds sound like 50/50?
It’s a bit un-intuitive, but you will actually have a higher chance of winning the car if you switch. Not a 1 in 2 chance of winning, but actually 2 out of 3 chance. If you don’t switch, then you will only win 1 in 3 times.
Not convinced?
Have a play with the demo at https://stuon.github.io/js-monty-hall-problem/. You can also use the 1000x simulate to compare the two results.
So why is this so?
Well let’s look at the first scenario of not switching. If you pick a random door from the three. And behind one door is a car, whilst the others are goats, you will have a 1 in 3 chance of winning the car. Ie number_of_cars / number_of_doors
Now let’s look at the second scenario of switching. When you choose a door at the start, you have a 1 in 3 chance of picking the car. Or from the other side, it also means you have a 2 in 3 chance of picking the goat. Think about this for a bit, as it’s important for the next part for the explanation. If you pick a goat, then the host will open another door with the second goat, which means the last unopened door will be a car. So if you switch, the odds of picking the car is the odds that you picked the goat in the first selection. Ie 2 in 3.
Diagram
Let’s assume the door looks like below and play through all the possible actions you can do.
| Door 1 | Door 2 | Door 3 |
| Goat | Goat | Car |
Possible selections
Not switching
| Door 1 | Door 2 | Door 3 | Strategy | Out Come |
| Goat | Goat | Car | Pick Door 1 | Lose |
| Goat | Goat | Car | Pick Door 2 | Lose |
| Goat | Goat | Car | Pick Door 3 | Win |
Non switching method
So out of the 3 possibilities, you can only win in 1 of them. So you have a 1 in 3 chance of winning.
Switching
| Door 1 | Door 2 | Door 3 | Strategy | Out Come |
| Goat | Goat | Car | Pick Door 1 | Win |
| Goat | Goat | Car | Pick Door 2 | Win |
| Goat | Goat | Car | Pick Door 3 | Lose |
Switching method
In this method, you can win in 2 of the possibilities. So you have a 2 in 3 chance of winning.
While the example above assumes the door started with “goat | goat | car”. you can will get same results if it was “car | goat | goat” or “goat | car | goat”.
Online Demo
https://stuon.github.io/js-monty-hall-problem/